
As numbers go, π is something of a celebrity. This is especially true today, which has been celebrated since the late 1980s (and officially since 2009) as Pi Day.
Despite all the attention, however, there are serious misconceptions about this number that really bug me as someone who works with numbers every day (and teaches about them on occasion).
Misconception 1: π = 3.14
This misconception comes from a very basic misunderstanding of the idea of an irrational number. On one level this is very understandable – most people encounter π long before they encounter any other irrational numbers, and the term irrational is confusing right up to the point of being misleading, so I should stop and explain the terminology a bit first.
In the language of mathematics (borrowed in this case from the language of Latin), a ratio is a number which expresses a relationship between two other numbers. A common everyday ratio is the number one half, which we commonly encounter written symbolically as ½ or 0.5. The ratio one half shows the relationship between the number one as a subset of the number two (hence ½), which is also the same as the relationship between the number five as a subset of the number ten (hence 0.5).
Irrational numbers can still actually be ratios, and they are definitely rational in the other English sense of the word (i.e., logical). What makes them irRATIONnal is that they can’t be expressed as the ratio of two whole numbers. π is, in fact, a ratio, but it is an irrational number. It is the ratio between the diameter of a circle and the circumference of the same circle. The problem is that whenever the diameter of a circle is a whole number, the circumference is not a whole number, and whenever the circumference is a whole number the diameter is not a whole number. This is frustrating to those of us who want things to be nice, neat, and tidy, but it shouldn’t really surprise us. After all, if you think about measuring lengths with a ruler, it is normal for these lengths not to come out as whole numbers of inches or centimeters. If anything, the overwhelming majority of natural objects do not have whole-number lengths and the overwhelming majority of numbers in the real world are irrational numbers (π is in good company).
Anyway, because irrational numbers in general are misunderstood, it is common for people to talk about π as if it were a rational number. There are lots of rational numbers that are relatively close to the number π. The most famous nearby rational number is probably 3.14 (which is off by around 1.3%), but 3 1/7 is even closer (off by a little less than half a percent). While these are the most common, there are lots of other rational numbers hanging out in the neighborhood. As a practical matter, using an approximation in place of π is good enough for rough estimation, but you should be careful not to rely on approximations if you are working on anything really big or really important.
In this day and age, any calculator or internet-capable device (most of us have a phone in our pocket already) can give us a much more accurate approximation, so why bother writing approximations when you can just write the number itself? Writing the symbol π uses less paper, less ink, and fewer pixels than 3.14, so why waste time on approximations?
Misconception 2: π is Special
As I mentioned already, π is really a very ordinary number. Sure, it can’t be written as a fraction or a decimal (which is why we need to borrow a handy Greek letter to write it), but it’s just the relationship between the diameter of any circle and the circumference of the same circle. Sure, it’s a useful number (any time we are dealing with circles, turns, or angles) but it isn’t magical and it doesn’t really behave any differently than any other irrational number. People don’t go around making artsy or bizarre movies about the square root of 15 or memorize the first 100 digits of the ratio of one side of a decagon to the diagonal.
Misconception 3: π is the Most Useful Ratio in a Circle
If my first peeve is one that is shared by almost all math teachers and my second may have offended a few people, this third one puts me in a definite but growing minority and just might earn me some hate mail. To put it simply, the ratio of the circumference of a circle to its diameter is interesting and useful. While I’ll grant that diameters are slightly easier to measure than radii, that’s no excuse for wasting centuries worth of math education focusing on π when there is a much more useful number lurking in the background which wasn’t even given a name until very recently. I refer, of course, to the number τ (tau).
τ, the ratio of the circumference of a circle to its radius is exactly twice the value of π, since the diameter of a circle is twice the value of the radius. Like π, it can be approximated to a nearby rational number like 6 1/7 or 6.28, but as with π, why bother with approximations? In the context of circle geometry, τ is slightly more useful than π ( τr for the circumference formula and 1/2 τr² for the area), but it really shines when it comes to understanding angles.
Radians, the most natural way of measuring angles, can be confusing when expressed using π, but are crystal-clear when expressed using τ. Since a radian is defined as an arc with the length of a radius, it makes sense that the number of radians making up a complete turn (full circle) is τ, the ratio of the circumference to the length of the radius. Just compare these two diagrams:
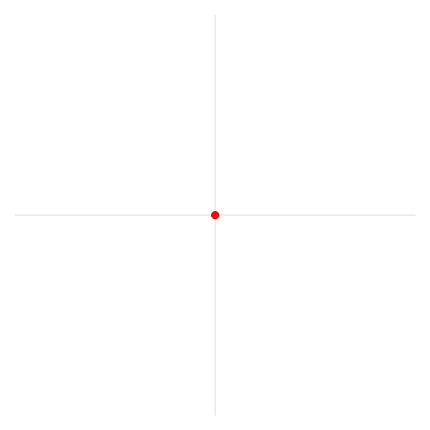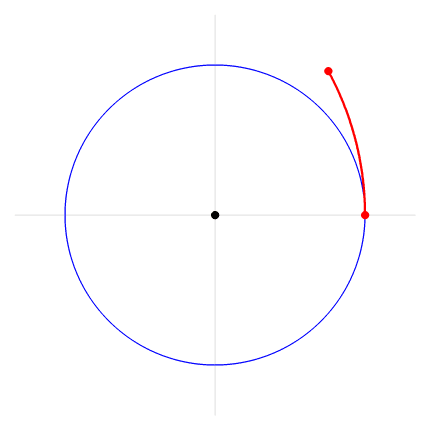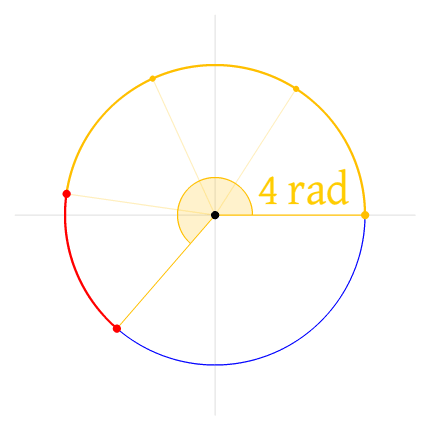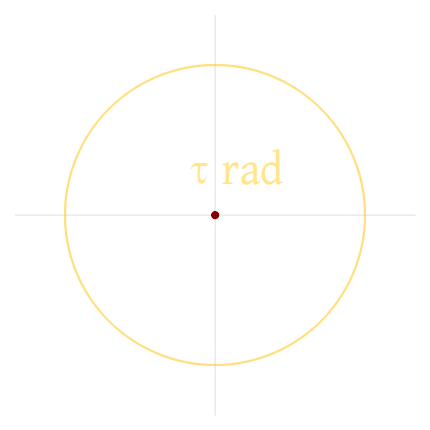

I think you will agree that the first diagram (the one explaining everything in terms of a circle instead of a half-circle) is clearer, so why not celebrate that constant instead?
Misconception τ/2 – 3: Isaac Just Doesn’t Appreciate π
I do appreciate π. It is a perfectly nice and well-behaved number that can be useful in certain situations. I just think people make way too much fuss about it, and math students everywhere would be better off if we spent more time talking about other irrational constants like τ, e, and ln(1).
And yes, I know some mathematician out there is just itching to ask whether Euler’s identity would be as elegant without π, so I’ll save you the trouble. Yes, this is much better: e^iτ = 1. With that I rest my case.
BONUS
Vi Hart has some really great videos on YouTube, and two of them fit perfectly with this post. I’ll let you watch and learn for yourself what Pythagoras has to do with π). Enjoy!




Leave a Reply